04/07/2016
Clase N°21
Distribución de probabilidades discretas
Es la distribucion en la cual la variable puede tomar un número determinado de valores, estudian los modelos matemáticos para calcular la probabilidad en algunos problemas tipicos en los que intervienen variables aleatorias discretas. El objetivo es obtener una formula matematica f(x)para determinar los valores de probabilidad
TEOREMA DE CHEVISHEV Demuestra cómo la desviación estándar es indicadora de la dispersión de la distribución de una variable aleatoria, el matemático ruso Pafnuty Lvovich Chébyshev desarrolló un teorema en el que ofrece una garantía mínima acerca de la probabilidad de que una variable aleatoria asuma un valor dentro de k desviaciones estándar alrededor de la media. Para cualquier variable aleatoria X con media µ y desviación estándar ó, la probabilidad de que X tome un valor contenido en k desviaciones estándar de la media, siendo k una constante positiva cualquiera, es cuando menos
1 - 1/k²
Simbólicamente, el teorema se expresa de cualquiera de las siguientes maneras:
La desigualdad de Chébyshev es muy importante, ya que permite determinar los límites de las probabilidades de variables aleatorias discretas o continuas sin tener que especificar sus funciones de probabilidad. Este teorema asegura que la probabilidad de que una variable aleatoria se aleje de la media no más de k desviaciones estándar, es menor o igual a 1/k2 para algún valor de k >1. Aunque la garantía no siempre es muy precisa, la ventaja sobre este teorema es su gran generalidad por cuanto es aplicable a cualquier variable aleatoria con cualquier distribución de probabilidad, ya sea discreta o continua.
TEOREMA DE CHEVISHEV Demuestra cómo la desviación estándar es indicadora de la dispersión de la distribución de una variable aleatoria, el matemático ruso Pafnuty Lvovich Chébyshev desarrolló un teorema en el que ofrece una garantía mínima acerca de la probabilidad de que una variable aleatoria asuma un valor dentro de k desviaciones estándar alrededor de la media. Para cualquier variable aleatoria X con media µ y desviación estándar ó, la probabilidad de que X tome un valor contenido en k desviaciones estándar de la media, siendo k una constante positiva cualquiera, es cuando menos
1 - 1/k²
Simbólicamente, el teorema se expresa de cualquiera de las siguientes maneras:
La desigualdad de Chébyshev es muy importante, ya que permite determinar los límites de las probabilidades de variables aleatorias discretas o continuas sin tener que especificar sus funciones de probabilidad. Este teorema asegura que la probabilidad de que una variable aleatoria se aleje de la media no más de k desviaciones estándar, es menor o igual a 1/k2 para algún valor de k >1. Aunque la garantía no siempre es muy precisa, la ventaja sobre este teorema es su gran generalidad por cuanto es aplicable a cualquier variable aleatoria con cualquier distribución de probabilidad, ya sea discreta o continua.
La desigualdad de Chébyshev es muy importante, ya que permite determinar los límites de las probabilidades de variables aleatorias discretas o continuas sin tener que especificar sus funciones de probabilidad. Este teorema asegura que la probabilidad de que una variable aleatoria se aleje de la media no más de k desviaciones estándar, es menor o igual a 1/k2 para algún valor de k >1. Aunque la garantía no siempre es muy precisa, la ventaja sobre este teorema es su gran generalidad por cuanto es aplicable a cualquier variable aleatoria con cualquier distribución de probabilidad, ya sea discreta o continua.
DISTRIBUCIÓN DISCRETA UNIFORME
La distribución o modelo uniforme puede considerarse como proveniente de un proceso de extracción aleatoria .El planteamiento radica en el hecho de que la probabilidad se distribuye uniformemente a lo largo de un intervalo . Así : dada una variable aleatoria continua, x , definida en el intervalo [a,b] de la recta real, diremos que x tiene una distribución uniforme en el intervalo [a,b] cuando su función de densidad para
06/07/2016
clase N°22
DISTRIBUCIÓN DISCRETA UNIFORME
- La distribución o modelo uniforme puede considerarse como proveniente de un proceso de extracción aleatoria .El planteamiento radica en el hecho de que la probabilidad se distribuye uniformemente a lo largo de un intervalo . Así : dada una variable aleatoria continua, x , definida en el intervalo [a,b] de la recta real, diremos que x tiene una distribución uniforme en el intervalo [a,b] cuando su función de densidad para
06/07/2016
clase N°22
DISTRIBUCIÓN DE BERNOULLI En teoría de probabilidad y estadística, la distribución de Bernoulli, es una distribución de probabilidad discreta, que toma valor 1 para la probabilidad de éxito (p) y valor 0 para la probabilidad de fracaso (q = 1 − p). Si X es una variable aleatoria que mide "número de éxitos", y se realiza un único experimento con dos posibles resultados (éxito o fracaso), se dice que la variable aleatoria X se distribuye como una Bernoulli de parámetro p. 
DISTRIBUCIÓN DE BERNOULLI En teoría de probabilidad y estadística, la distribución de Bernoulli, es una distribución de probabilidad discreta, que toma valor 1 para la probabilidad de éxito (p) y valor 0 para la probabilidad de fracaso (q = 1 − p). Si X es una variable aleatoria que mide "número de éxitos", y se realiza un único experimento con dos posibles resultados (éxito o fracaso), se dice que la variable aleatoria X se distribuye como una Bernoulli de parámetro p.
11/07/2016
clase N°23
DISTRIBUCIÓN BINOMIAL
Esta distribución es muy importante y de uso frecuente. Corresponde a experimentos con características similares a un experimento Bernoulli, pero ahora es de interés la variable aleatoria relacionada con la cantidad de éxitos que se obtienen en un experimento.
Características de un experimento Binomial:
La cantidad de ensayos n, que se realiza es finita, Cada ensayo tiene únicamente dos resultados posibles, Todos los ensayos realizados son independientes, La probabilidad p. de obtener éxito en cada ensayo es constante
DISTRIBUCIÓN BINOMIAL NEGATIVA.
Esta distribución puede considerarse como una extensión o ampliación de la distribución geométrica . La distribución binomial negativa es un modelo adecuado para tratar aquellos procesos en los que se repite un determinado ensayo o prueba hasta conseguir un número determinado de resultados favorables (por vez primera) .Es por tanto de gran utilidad para aquellos muestreos que procedan de esta manera. Si el número de resultados favorables buscados fuera 1 estaríamos en el caso de la distribución geométrica . Está implicada también la existencia de una dicotomía de resultados posibles en cada prueba y la independencia de cada prueba o ensayo, o la reposición de los individuos muestreados.
El proceso consta de un número no definido de pruebas separadas o separables . El proceso concluirá cuando se obtenga un determinado número de resultados favorables K
· Cada prueba puede dar dos resultados posibles mutuamente excluyentes A y no A
· La probabilidad de obtener un resultado A en cada una de las pruebas es p siendo la probabilidad de no A , q . Lo que nos lleva a que p+q=1
· Las probabilidades p y q son constantes en todas las pruebas. Todas las pruebas son independientes. Si se trata de un experimento de extracción éste se llevará cabo con devolución del individuo extraído, a no ser que se trate de una población en la que el número de individuos tenga de carácter infinito.
· (Derivación de la distribución) Si, en estas circunstancias aleatorizamos de forma que la variable aleatoria x sea "el número de pruebas necesarias para conseguir K éxitos o resultados A " ; entonces la variable aleatoria x seguirá una distribución binomial negativa con parámetros p y k
será entonces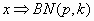 
La variable aleatoria x podrá tomar sólo valores superiores a k 
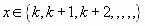El suceso del que se trata podría verse como:
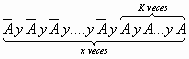Media y varianza de la distribución Binomial Negativa
11/07/2016
clase N°23
DISTRIBUCIÓN BINOMIAL
Esta distribución es muy importante y de uso frecuente. Corresponde a experimentos con características similares a un experimento Bernoulli, pero ahora es de interés la variable aleatoria relacionada con la cantidad de éxitos que se obtienen en un experimento.
Características de un experimento Binomial:
La cantidad de ensayos n, que se realiza es finita, Cada ensayo tiene únicamente dos resultados posibles, Todos los ensayos realizados son independientes, La probabilidad p. de obtener éxito en cada ensayo es constante
DISTRIBUCIÓN BINOMIAL NEGATIVA.
Esta distribución puede considerarse como una extensión o ampliación de la distribución geométrica . La distribución binomial negativa es un modelo adecuado para tratar aquellos procesos en los que se repite un determinado ensayo o prueba hasta conseguir un número determinado de resultados favorables (por vez primera) .Es por tanto de gran utilidad para aquellos muestreos que procedan de esta manera. Si el número de resultados favorables buscados fuera 1 estaríamos en el caso de la distribución geométrica . Está implicada también la existencia de una dicotomía de resultados posibles en cada prueba y la independencia de cada prueba o ensayo, o la reposición de los individuos muestreados.
El proceso consta de un número no definido de pruebas separadas o separables . El proceso concluirá cuando se obtenga un determinado número de resultados favorables K
· Cada prueba puede dar dos resultados posibles mutuamente excluyentes A y no A
· La probabilidad de obtener un resultado A en cada una de las pruebas es p siendo la probabilidad de no A , q . Lo que nos lleva a que p+q=1
· Las probabilidades p y q son constantes en todas las pruebas. Todas las pruebas son independientes. Si se trata de un experimento de extracción éste se llevará cabo con devolución del individuo extraído, a no ser que se trate de una población en la que el número de individuos tenga de carácter infinito.
· (Derivación de la distribución) Si, en estas circunstancias aleatorizamos de forma que la variable aleatoria x sea "el número de pruebas necesarias para conseguir K éxitos o resultados A " ; entonces la variable aleatoria x seguirá una distribución binomial negativa con parámetros p y k
será entonces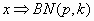
La variable aleatoria x podrá tomar sólo valores superiores a k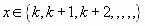
El suceso del que se trata podría verse como:
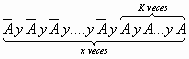
Media y varianza de la distribución Binomial Negativa
13/07/2016
clase N°24
DISTRIBUCIÓN HIPERGEOMÉTRICA
- Se aplica cuando la muestra (n) es una proporción relativamente grande en relación con la población (n > 0.1N). El muestreo se hace sin reemplazo
- P(x,N,n,D) es la probabilidad de exactamente x éxitos en una muestra de n elementos tomados de una población de tamaño N que contiene D éxitos. La función de densidad de distribución hipergeométrica:
La media y la varianza de la distribución hipergeométrica son:
- Se aplica cuando la muestra (n) es una proporción relativamente grande en relación con la población (n > 0.1N). El muestreo se hace sin reemplazo
- P(x,N,n,D) es la probabilidad de exactamente x éxitos en una muestra de n elementos tomados de una población de tamaño N que contiene D éxitos. La función de densidad de distribución hipergeométrica:
La media y la varianza de la distribución hipergeométrica son:
Media y varianza de la distribución Hipergeométrica
18/07/2016
clase N° 25
DISTRIBUCIÓN DE POISSON
La distribución de Poisson es un modelo que puede usarse para calcular la probabilidad correspondiente al numero de éxitos que se obtendrían en una región o en intervalo de tiempos especificados, si se conoce el numero promedio de éxitos que ocurren.
Este modelo requiere que se cumplan las siguientes suposiciones:
a) El número de éxitos que ocurren en la region o intervalo es independiente de o que ocurre en otra region o intervalo.
b) La probabilidad de que un resultado ocurra en una region o intervalo muy pequeño, es igual para todos los intervalo o regiones de igual tamaño y es proporcional al tamaño de a region o intervalo.
c) La probabilidad de que mas de un resultado ocurra en una región o intervalo muy pequeño no es significativa.
MEDIA Y VARIANZA DE LA DISTRIBUCION DE POISSON.
VARIABLES ALEATORIAS CONTINUAS
Las variables aleatorias continuas definen reglas de correspondencia entre los resultados obtenidos en experimentos cuyos valores se miden en una escala continua y el conjunto de los números reales.
Función de Densidad de Probabilidad
La probabilidad de un variables aleatoria continua puede especificarse si existe una función de densidad de probabilidad, tal que el area debajo de la grafica sea una función que cumpla los requisitos para que sea una medida del valor de probabilidad.
Propiedades de una función de Densidad de Probabilidad
25/07/2016
clase N°26
Media y varianza de la distribución Hipergeométrica
18/07/2016
clase N° 25
La distribución de Poisson es un modelo que puede usarse para calcular la probabilidad correspondiente al numero de éxitos que se obtendrían en una región o en intervalo de tiempos especificados, si se conoce el numero promedio de éxitos que ocurren.
Este modelo requiere que se cumplan las siguientes suposiciones:
a) El número de éxitos que ocurren en la region o intervalo es independiente de o que ocurre en otra region o intervalo.
b) La probabilidad de que un resultado ocurra en una region o intervalo muy pequeño, es igual para todos los intervalo o regiones de igual tamaño y es proporcional al tamaño de a region o intervalo.
c) La probabilidad de que mas de un resultado ocurra en una región o intervalo muy pequeño no es significativa.
MEDIA Y VARIANZA DE LA DISTRIBUCION DE POISSON.
VARIABLES ALEATORIAS CONTINUAS
Las variables aleatorias continuas definen reglas de correspondencia entre los resultados obtenidos en experimentos cuyos valores se miden en una escala continua y el conjunto de los números reales.
Función de Densidad de Probabilidad
La probabilidad de un variables aleatoria continua puede especificarse si existe una función de densidad de probabilidad, tal que el area debajo de la grafica sea una función que cumpla los requisitos para que sea una medida del valor de probabilidad.
Propiedades de una función de Densidad de Probabilidad
25/07/2016
clase N°26
DISTRIBUCIÓN EXPONENCIAL Se usa para modelar artículos con una tasa de falla constante y está relacionada con la distribución de Poisson. Si una variable aleatoria x se distribuye exponencialmente, entonces el recíproco de x, y = 1/x sigue una distribución de Poisson y viceversa. La función de densidad de probabilidad exponencial es: Para x >= 0
La función de densidad de la distribución exponencial
El modelo exponencial, con un solo parámetro, es el más simple de todos los modelos de distribución del tiempo de vida. Las ecuaciones clave para la exponencial se muestran:
La función de densidad de la distribución exponencial
El modelo exponencial, con un solo parámetro, es el más simple de todos los modelos de distribución del tiempo de vida. Las ecuaciones clave para la exponencial se muestran:
DISTRIBUCIONES DE PROBABILIDAD CONTINUAS
En esta sección se estudio algunos de los modelos mas importantes para calcular la probabilidad en algunos problemas típicos en los que intervienen variables aleatorias continuas.
El objetivo es obtener una formula matemática f(x) para determinar los valores de probabilidad de la variable aleatoria X.
1. Distribución Uniforme Continua
Este modelo corresponde a una variable aleatoria continua cuyos valores tienen igual valor de probabilidad en un intervalo especificado para la variable
27/07/2016
Clase N°27
MUESTREO ESTADISTICO
El muestreo estadístico es un procedimiento para obtener datos de una población con la finalidad de usar esta información para realizar inferencias acerca de dicha población mediante las técnicas que se estudian en Estadística Inferencial.
Las muestras son subconjunto de los datos. El conjunto de todas las muestras que se pueden obtener de la población se denomina espacio muestral.
El muestreo estadístico se basa en el principio de equiprobabilidad, es decir que cada individuo de la población tiene la misma probabilidad de ser elegido. Consecuentemente, cada muestra también tendrá la misma probabilidad de ser seleccionada.
Para obtener conclusiones y evidencias comprobatorias suficientes, el investigador no esta obligado a examinar todos y cada uno de los individuos o muestras de una población. Solamente debe examinar una muestra representativa de dicha población
DISTRIBUCIONES DE PROBABILIDAD CONTINUAS
En esta sección se estudio algunos de los modelos mas importantes para calcular la probabilidad en algunos problemas típicos en los que intervienen variables aleatorias continuas.
El objetivo es obtener una formula matemática f(x) para determinar los valores de probabilidad de la variable aleatoria X.
1. Distribución Uniforme Continua
Este modelo corresponde a una variable aleatoria continua cuyos valores tienen igual valor de probabilidad en un intervalo especificado para la variable
27/07/2016
Clase N°27
El muestreo estadístico es un procedimiento para obtener datos de una población con la finalidad de usar esta información para realizar inferencias acerca de dicha población mediante las técnicas que se estudian en Estadística Inferencial.
Las muestras son subconjunto de los datos. El conjunto de todas las muestras que se pueden obtener de la población se denomina espacio muestral.
El muestreo estadístico se basa en el principio de equiprobabilidad, es decir que cada individuo de la población tiene la misma probabilidad de ser elegido. Consecuentemente, cada muestra también tendrá la misma probabilidad de ser seleccionada.
Para obtener conclusiones y evidencias comprobatorias suficientes, el investigador no esta obligado a examinar todos y cada uno de los individuos o muestras de una población. Solamente debe examinar una muestra representativa de dicha población
TEOREMA DE LÍMITE CENTRAL
El teorema del límite central es un teorema fundamental de probabilidad y estadística. El teorema establece que la distribución de, que es la media de una muestra aleatoria de una población con varianza finita, tiene una distribución aproximadamente normal cuando el tamaño de la muestra es grande, independientemente de la forma de la distribución de la población. Muchos procedimientos estadísticos comunes requieren que los datos sean aproximadamente normales, pero el teorema del límite central le permite aplicar estos procedimientos útiles a poblaciones que son marcadamente no normales. El tamaño que debe tener la muestra depende de la forma de la distribución original. Si la distribución de la población es simétrica, un tamaño de muestra de 5 podría generar una aproximación adecuada; si la distribución de la población es marcadamente asimétrica, se requiere un tamaño de muestra de 50 o más. Las siguientes gráficas muestran ejemplos de cómo la distribución afecta el tamaño de la muestra que usted necesita.
El teorema del límite central es un teorema fundamental de probabilidad y estadística. El teorema establece que la distribución de, que es la media de una muestra aleatoria de una población con varianza finita, tiene una distribución aproximadamente normal cuando el tamaño de la muestra es grande, independientemente de la forma de la distribución de la población. Muchos procedimientos estadísticos comunes requieren que los datos sean aproximadamente normales, pero el teorema del límite central le permite aplicar estos procedimientos útiles a poblaciones que son marcadamente no normales. El tamaño que debe tener la muestra depende de la forma de la distribución original. Si la distribución de la población es simétrica, un tamaño de muestra de 5 podría generar una aproximación adecuada; si la distribución de la población es marcadamente asimétrica, se requiere un tamaño de muestra de 50 o más. Las siguientes gráficas muestran ejemplos de cómo la distribución afecta el tamaño de la muestra que usted necesita.
No hay comentarios:
Publicar un comentario